（仅作个人备忘）

其实很早就想着更了，但是因为前段时间封校导致没法更新，现在趁着上网课就更新吧。

PS: KaTeX\textbf{ \KaTeX}终于弄好了！！！

基本结构

1
2
3
4
5
6
#include <bits/stdc++.h>
using namespace std;
int main(){
    //代码
    return 0;
}

排序

STLsort

最香的当然是STL sort，采用快排堆排插排混合，时间复杂度O(nlogn)O(n log_{n} )到O(n2)O(n^2)：

1
2
sort(arr,arr+n,cmp);
//其中cmp可以不加，默认从小到大

至于cmp的写法,只需要写两项的比较规则，比如从小到大写成:

1
2
3
int cmp(int a,int b){
    return a<b;
}

从大到小：

1
2
3
int cmp(int a,int b){
    return a>b;
}

利用cmp就能实现sort的结构体排序和题目的特殊要求，举个例子：

例子

FZQOJ#84. 近似排序

读入正整数x和y，将这两个数之间（包括这两个数本身）的所有数按下述特别规则排序后输出。

该特别规则是：按两数倒过来的值进行比较决定其大小，如30倒过来为3,29倒过来为92，则29大于30

【输入】
一行两个整数x和y，用一个空格隔开，1≤x≤y≤10000000001\le x\le y\le 1000000000,y−x≤100y-x\le 100

【输出】
包括y−x+1y-x+1行，每行一个正整数，按两数倒过来的值进行比较决定其大小，然后由小到大输出

【样例】
样例输入1

1
22 39

样例输出1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
30
31
22
32
23
33
24
34
25
35
26
36
27
37
28
38
29
39

使用sort：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;
int cmp(int a,int b){
    int a2=0;
    while(a!=0)
    { 
        a2*=10;
        a2+=a%10;
        a/=10;
    }
    int b2=0;
    while(b!=0)
    { 
        b2*=10;
        b2+=b%10;
        b/=10;
    }
    return a2<b2;
}
int main(){
    int x,y,l[114];
    cin>>x>>y;
    int n=y-x+1;
    for(int i=1;i<=n;i++){
        l[i]=i+x-1;
    }
    sort(l+1,l+n+1,cmp);
    for(int i=1;i<=n;i++){
        cout<<l[i]<<endl;
    }
    return 0;
}

冒泡：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;
int cmp(int a,int b){
    int a2=0;
    while(a!=0)
    { 
        a2*=10;
        a2+=a%10;
        a/=10;
    }
    int b2=0;
    while(b!=0)
    { 
        b2*=10;
        b2+=b%10;
        b/=10;
    }
    return a2<b2;
}
int main(){
    int x,y,l[114];
    cin>>x>>y;
    int n=y-x+1;
    for(int i=1;i<=n;i++){
        l[i]=i+x-1;
    }
    for(int i=2;i<=n;i++){
        for(int j=2;j<=n;j++){
            if(cmp(l[j],l[j-1])){
                int tmp=l[j];
                l[j]=l[j-1];
                l[j-1]=tmp;
            }
        }
    }
    for(int i=1;i<=n;i++){
        cout<<l[i]<<endl;
    }
    return 0;
}

都是AC代码，但是显然前者速度更快且更简单，可以节省你在比赛时的时间以及突然忘记模板的风险。

选择排序

时间复杂度：固定时间复杂度O(n2)O(n^2)，不稳定

我使用的是打擂台一个一个找放到第二个数组中，这样子可以简单一点，当然空间复杂度双倍快乐

实测选排比冒泡快，因为冒泡要交换

从大到小：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int arr[114514],arr2[191981],n,max,maxi,k=1;
//freopen("random.in","r",stdin);
//freopen("random.out","w",stdout); 
scanf("%d",&n);
for(int i=1;i<=n;i++){
    scanf("%d",&arr[i]);
}
//n为数组长度
for(int i=1;i<=n;i++){
    max=0x7FFFFFFF;
    for(int j=1;j<=n;j++){
        if(arr[j]>max){
            max=arr[j];
            maxi=j;
        }
    }
    arr[maxi]=0x7FFFFFFF;
    arr2[k]=max;
    k++;
}
for(int i=1;i<=n;i++){
    printf("%d ",arr2[i]);
} //输出

从小到大：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int arr[114514],arr2[191981],n,min,mini,k=1;
//freopen("random.in","r",stdin);
//freopen("random.out","w",stdout); 
scanf("%d",&n);
for(int i=1;i<=n;i++){
    scanf("%d",&arr[i]);
}
//n为数组长度
for(int i=1;i<=n;i++){
    min=0x7FFFFFFF;
    for(int j=1;j<=n;j++){
        if(arr[j]<min){
            min=arr[j];
            mini=j;
        }
    }
    arr[mini]=0x7FFFFFFF;
    arr2[k]=min;
    k++;
}
for(int i=1;i<=n;i++){
    printf("%d ",arr2[i]);
} //输出

冒泡排序

时间复杂度：固定O(n2)O(n^2)，具有稳定性。

一个板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int arr[114514],n;
//freopen("random.in","r",stdin);
//freopen("random.out","w",stdout); 
scanf("%d",&n);
for(int i=1;i<=n;i++){
    scanf("%d",&arr[i]);
}
for(int i=2;i<=n;i++){
    for(int j=2;j<=n;j++){
        if(arr[j]>arr[j-1]){ //从小到大则把符号改为<
            int tmp=arr[j];
            arr[j]=arr[j-1];
            arr[j-1]=tmp;
        }
    }
}
for(int i=1;i<=n;i++){
    printf("%d ",arr[i]);
} //输出

桶排序

较为简单，不稳定，时间复杂度O(n)O(n)，空间复杂度较高，不适用于结构体和小数。

PS：这个桶排序指标记桶，并不是说分治的那个桶排序

2022.11.16更新

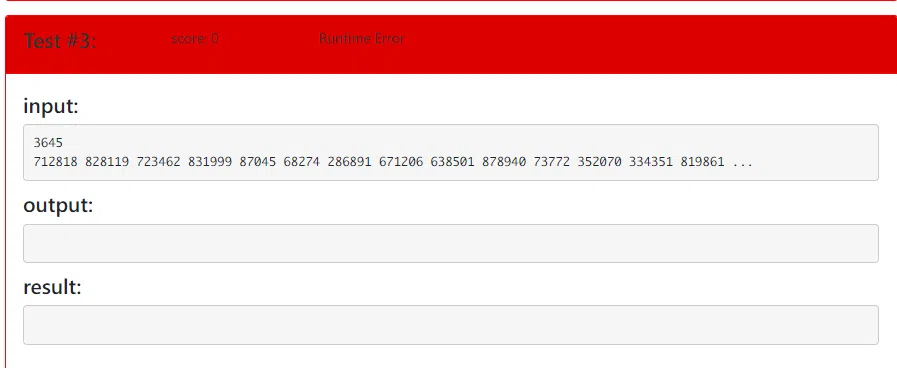
发现标记范围bug，已修正，然而本地能过（试过n=10000的数据规模也没有tle）但是过不了板子题qwq

1668570918842.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int arr[114514],bucket[114514],arr2[114514],n,k=1;
//freopen("random.in","r",stdin);
//freopen("random.out","w",stdout); 
scanf("%d",&n);
for(int i=1;i<=n;i++){
    scanf("%d",&arr[i]);
}
//arr指待排序数组，n为长度
for(int i=0;i<114514;i++){
    bucket[i]=0;
}
for(int i=1;i<=n;i++){
    bucket[arr[i]]++;
}
for(int i=0;i<114514;i++){ //从大到小改为for(int i=114513;i>=0;i--)
    for(int j=1;j<=bucket[i];j++){
        arr2[k]=i; //也可以直接输出，写成：cout<<i<<" ";
        k++;
    }
}
for(int i=1;i<=n;i++){
    cout<<arr2[i]<<" ";
} //输出

就是在有序数组中做标记，和稳定完全搭不上边耶欸欸欸。

简单数论

斐波那契数列

求第nn项

数组

1
2
3
4
5
6
int n,l[114]={0,1};
cin>>n;
for(int i=2;i<=n;i++){
    l[i]=l[i-1]+l[i-2];
}
cout<<l[n];

递归

PS：时间复杂度O(n2)O(n^2)，不建议使用

1
2
3
4
5
6
7
8
9
int fibnacci(int n) {
    if(n < 1) {
        return 0;
    }else if(n == 1 || n == 2) {
        return 1;
    }
 
    return f1(n-1) + f1(n-2);
}

递推（空间复杂度O(1)O(1)）

1
2
3
4
5
6
7
8
int k,n=1,a=1,b=1;
cin>>k;
for(int i=3;i<=k;i++){
    n=a+b;
    a=b;
    b=n;
}
cout<<n;

质数

咕咕咕。。。

拆数

1
2
3
4
5
6
7
int a=n,l=1,arr[114];
while(a!=0){
    arr[l]=a%10;
    a/=10;
    l++;
}
l--;

快读快写

这些在一堆数据动不动就TLE的题中很好用，比scanf,printf，cin,cout快

快读板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void read(int &n){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    n=x*f;
}

快写板子：

1
2
3
4
5
6
7
8
inline void print(int n){
    if(n<0){
        putchar('-');
        n*=-1;
    }
    if(n>9) print(n/10);
    putchar(n % 10 + '0');
}

原理就是getchar，然后int和char互转

当然如果要用lld或者int128的话改一下也行的啦

求最大公约数

穷举

穷举么？雀食可以，不过

搜索

搜索虽然我背得模板但是用的不太熟悉qwq，依然是穷举贪心tle，然后助我退役

1668133472932.png

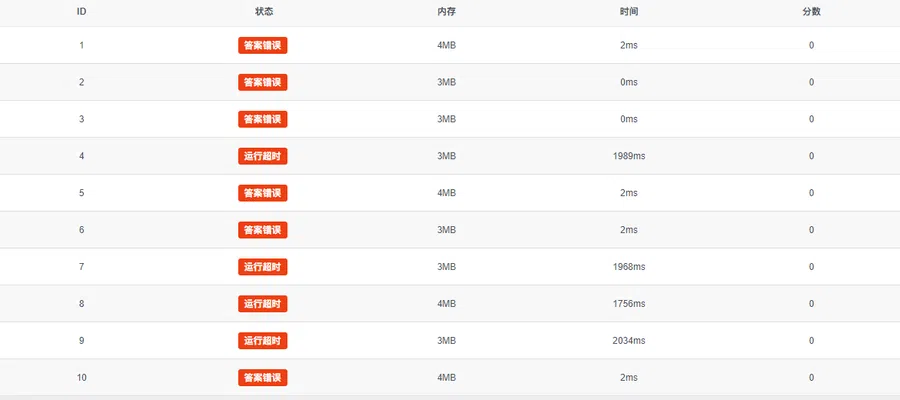
1668133599340.png

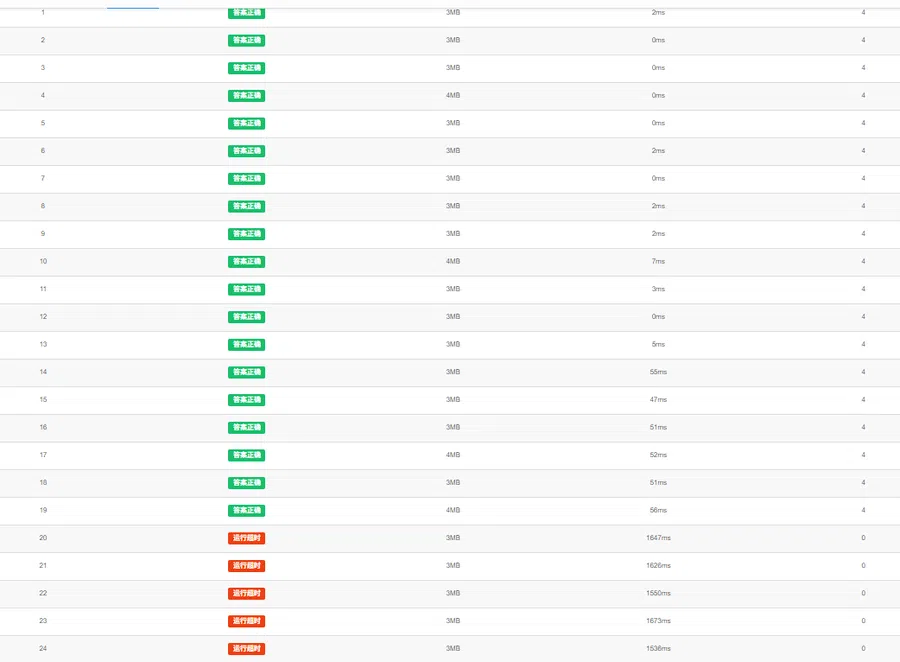
1668133671028.png

1668133741932.png

笑死。

二分

姑且也算搜索放进来吧。

原理就是根据大小不断分段。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int binarySearch(int arr[],int p,int q,int t) {
    int mid=0;
    if(p>q) {
        return -1;
    }
    mid=p+(q-p)/2;
    if(t==arr[mid]) {
        return mid;
    }
    if(t<arr[mid]) { //降序改为>
        return binarySearch(arr,p,mid-1,t);
    }
    else{
        return binarySearch(arr,mid+1,q,t);
    }
}

DFS

DFS比BFS貌似好理解点，因为是递归，一个费stack一个费queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int dfs(int t)
{
    if(满足返回条件)
    {
        return 解;
    }
    else
    {
        for(int i=1;i<=尝试方法数;i++)
            if(满足进一步搜索条件)
            {
                为进一步搜索所需要的状态打上标记;
                dfs(t+1);
                回溯一步;
            }
    }
}

BFS

这个真不会算了…

DP

no，我不会ヾ(´･ ･｀｡)ノ"

数据结构

链表

明天再写未完待续…

(PS：这篇文章充分体现了我OI的垃圾)
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、