CSP-J 2023 题解

考完了CSP之后，自然是打算写题解了，因为今年没参加S组qwq，所以就只写了J组的TJ。

T1 apple

题目

点击展开题目

题目描述

小 Y 的桌子上放着 $n$ 个苹果从左到右排成一列，编号为从 $1$ 到 $n$。

小苞是小 Y 的好朋友，每天她都会从中拿走一些苹果。

每天在拿的时候，小苞都是从左侧第 $1$ 个苹果开始、每隔 $2$ 个苹果拿走 $1$ 个苹果。随后小苞会将剩下的苹果按原先的顺序重新排成一列。

小苞想知道，多少天能拿完所有的苹果，而编号为 $n$ 的苹果是在第几天被拿走的？

输入格式

输入的第一行包含一个正整数 $n$，表示苹果的总数。

输出格式

输出一行包含两个正整数，两个整数之间由一个空格隔开，分别表示小苞拿走所有苹果所需的天数以及拿走编号为 $n$ 的苹果是在第几天。

样例 #1

样例输入 #1

8

样例输出 #1

5 5

提示

【样例 $1$ 解释】

小苞的桌上一共放了 $8$ 个苹果。
小苞第一天拿走了编号为 $1$、$4$、$7$ 的苹果。
小苞第二天拿走了编号为 $2$、$6$ 的苹果。
小苞第三天拿走了编号为 $3$ 的苹果。
小苞第四天拿走了编号为 $5$ 的苹果。
小苞第五天拿走了编号为 $8$ 的苹果。

【样例 $2$】

见选手目录下的 apple/apple2.in 与 apple/apple2.ans。

【数据范围】

对于所有测试数据有：$1\leq n\leq 10^9$。

测试点	$n\leq$	特殊性质
$1\sim 2$	$10$	无
$3\sim 5$	$10^3$	无
$6\sim 7$	$10^6$	有
$8\sim 9$	$10^6$	无
$10$	$10^9$	无

特殊性质：小苞第一天就取走编号为 $n$ 的苹果。

题解

还是很简单的一个找规律题。对于第一问，可以发现的是，每隔两个拿一个苹果的话，是相当于以 3 个苹果为一组，剩下不够 3 个的也当一组，每一次拿走一组中的第一个就可以了。

当 $n=8$ 时，图就是这样子的：

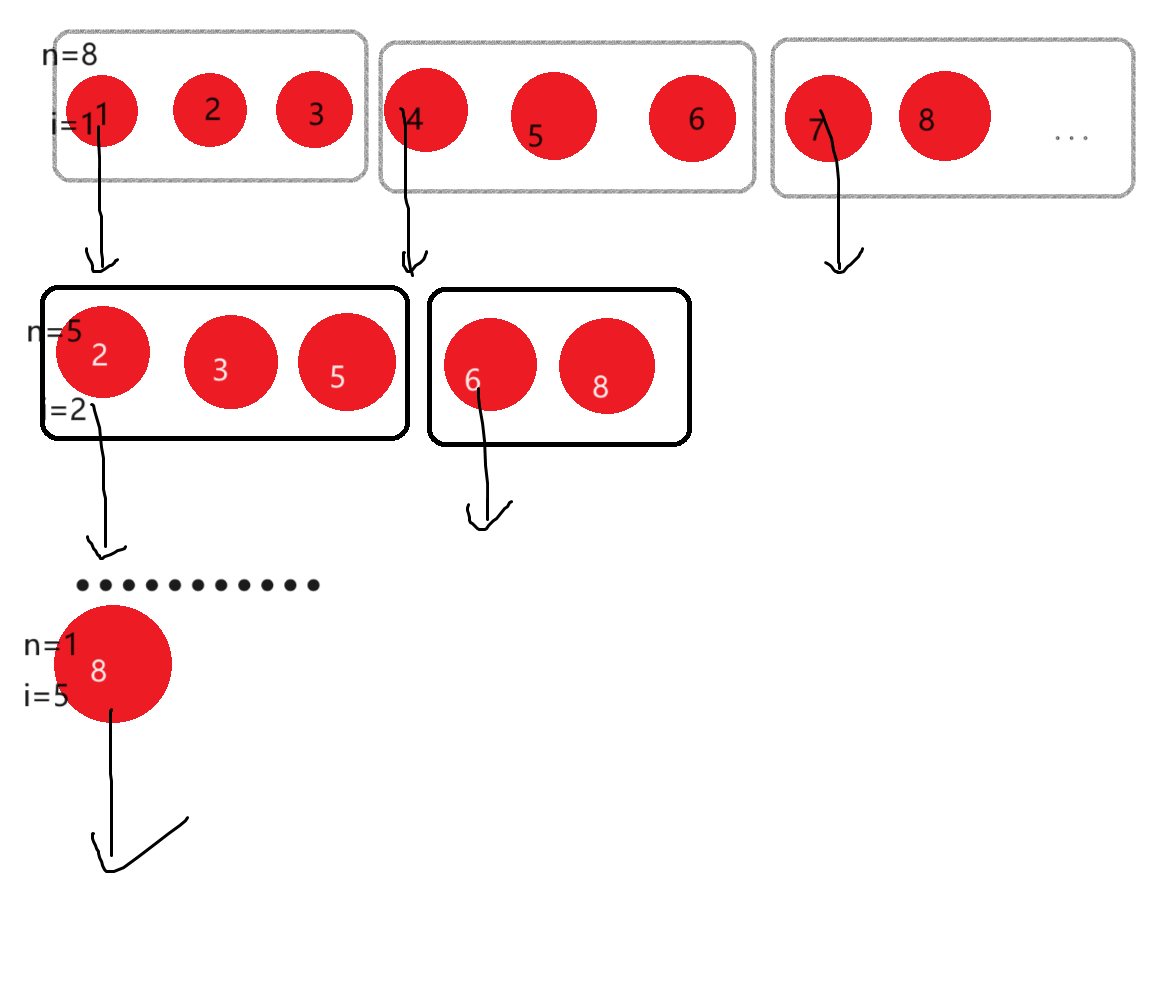
第二问呢？

根据上图可以发现，当 $i=5$ 时，$n \mod 3=1$，此时最后一组的第一个就是第 $n$ 个苹果了，直接输出 $i$ 就好。

代码

这是我的考场代码（增加了一些注释，有些是考场发癫写的）：

#include <bits/stdc++.h>
//能出1=么，能出300么qwq
//CQ-J00273 LYX
//签到水题，找规律：（
using namespace std;
int main(){
    freopen("apple.in","r",stdin);
    freopen("apple.out","w",stdout);
    long long n,i=0,ans=-1; //ans=-1标记ans未更新过
    cin>>n;
    while(n){
        if(n%3==1&&!~ans) ans=i+1; //!~ans判断ans是否为-1，如果未更新过ans，此时的i就是取到第n个苹果的时间戳
        n-=ceil(n*1.0/3),i++; //减掉3个一组第一个的苹果个数
    }
    cout<<i<<" "<<ans<<endl;
    //小知识：我平常不加endl，但是Linux下是没有自动换行的，看起来很难受。
    return 0;
}

T2 road

题面

点击查看题面

题目描述

小苞准备开着车沿着公路自驾。

公路上一共有 $n$ 个站点，编号为从 $1$ 到 $n$。其中站点 $i$ 与站点 $i + 1$ 的距离为 $v_i$ 公里。

公路上每个站点都可以加油，编号为 $i$ 的站点一升油的价格为 $a_i$ 元，且每个站点只出售整数升的油。

小苞想从站点 $1$ 开车到站点 $n$，一开始小苞在站点 $1$ 且车的油箱是空的。已知车的油箱足够大，可以装下任意多的油，且每升油可以让车前进 $d$ 公里。问小苞从站点 $1$ 开到站点 $n$，至少要花多少钱加油？

输入格式

输入的第一行包含两个正整数 $n$ 和 $d$，分别表示公路上站点的数量和车每升油可以前进的距离。

输入的第二行包含 $n - 1$ 个正整数 $v_1, v_2\dots v_{n-1}$，分别表示站点间的距离。

输入的第三行包含 $n$ 个正整数 $a_1, a_2 \dots a_n$，分别表示在不同站点加油的价格。

输出格式

输出一行，仅包含一个正整数，表示从站点 $1$ 开到站点 $n$，小苞至少要花多少钱加油。

样例 #1

样例输入 #1

5 4
10 10 10 10
9 8 9 6 5

样例输出 #1

79

提示

【样例 1 解释】

最优方案下：小苞在站点 $1$ 买了 $3$ 升油，在站点 $2$ 购买了 $5$ 升油，在站点 $4$ 购买了 $2$ 升油。

【样例 2】

见选手目录下的 road/road2.in 与 road/road2.ans。

【数据范围】

对于所有测试数据保证：$1 \leq n \leq 10^5$，$1 \leq d \leq 10^5$，$1 \leq v_i \leq 10^5$，$1 \leq a_i \leq 10^5$。

测试点	$n \leq$	特殊性质
$1\sim 5$	$8$	无
$6\sim 10$	$10^3$	无
$11\sim 13$	$10^5$	A
$14\sim 16$	$10^5$	B
$17\sim 20$	$10^5$	无

• 特殊性质 A：站点 $1$ 的油价最低。
• 特殊性质 B：对于所有 $1 \leq i < n$，$v_i$ 为 $d$ 的倍数。

题解

这道题思维难度稍高一点，需要一种贪心思想。

贪心思想大概如此：不按照原来的思路。先在第一个站加油到达第二个站，如果第二个站便宜就加第二个，不然还是加第一站的油，到了第三站之后也是在前三个站中找最便宜的加油去第四站，以此类推。

简单一点说就是对于第 $i$ 个加油站，把加油的单价替换为 $a_{\min{\{a\}}}$

然后模拟距离即可，注意油量和取整的问题。以及，一定要开 long long 和 double，不然你会死得很惨！（洛谷死的是75pts）

代码

下面是我的代码，包括考试发癫和后续加的注释。

#include <bits/stdc++.h>
//qwq 差点挂掉
#define int long long //不开longlong见祖宗
using namespace std;
int n,d,v[114514],a[114514],minn=1e9,ans; //两个数组作用如题，注意实际上a_n项是没有用的（因为都到了第n个站了就不需要再加油去其他地方了）
double yl=0;
signed main(){
    ios::sync_with_stdio(0);
    freopen("road.in","r",stdin);
    freopen("road.out","w",stdout);
    cin>>n>>d;
    for(int i=1;i<n;i++) cin>>v[i];
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<n;i++){ //注意 i<n，小学植树问题（
        minn=min(a[i],minn); //替换加油价格
        yl-=v[i-1]*1.0/d; //计算到了这个站的剩余油量
        ans+=ceil((v[i]-yl*d)/d)*minn; //计算加油量并算钱
        yl+=ceil((v[i]-yl*d)/d);
    }
    cout<<ans<<endl;
    return 0;
}

T3 uqe

题面

点击查看题面

题目背景

众所周知，对一元二次方程 $ax ^ 2 + bx + c = 0, (a \neq 0)$，可以用以下方式求实数解：

• 计算 $\Delta = b ^ 2 - 4ac$，则:
  1. 若 $\Delta < 0$，则该一元二次方程无实数解。
  2. 否则 $\Delta \geq 0$，此时该一元二次方程有两个实数解 $x _ {1, 2} = \frac{-b \pm \sqrt \Delta}{2a}$。

例如：

• $x ^ 2 + x + 1 = 0$ 无实数解，因为 $\Delta = 1 ^ 2 - 4 \times 1 \times 1 = -3 < 0$。
• $x ^ 2 - 2x + 1 = 0$ 有两相等实数解 $x _ {1, 2} = 1$。
• $x ^ 2 - 3x + 2 = 0$ 有两互异实数解 $x _ 1 = 1, x _ 2 = 2$。

在题面描述中 $a$ 和 $b$ 的最大公因数使用 $\gcd(a, b)$ 表示。例如 $12$ 和 $18$ 的最大公因数是 $6$，即 $\gcd(12, 18) = 6$。

题目描述

现在给定一个一元二次方程的系数 $a, b, c$，其中 $a, b, c$ 均为整数且 $a \neq 0$。你需要判断一元二次方程 $a x ^ 2 + bx + c = 0$ 是否有实数解，并按要求的格式输出。

在本题中输出有理数 $v$ 时须遵循以下规则：

• 由有理数的定义，存在唯一的两个整数 $p$ 和 $q$，满足 $q > 0$，$\gcd(p, q) = 1$ 且 $v = \frac pq$。

• 若 $q = 1$，则输出 {p}，否则输出 {p}/{q}，其中 {n} 代表整数 $n$ 的值；

• 例如：

  • 当 $v = -0.5$ 时，$p$ 和 $q$ 的值分别为 $-1$ 和 $2$，则应输出 -1/2；
  • 当 $v = 0$ 时，$p$ 和 $q$ 的值分别为 $0$ 和 $1$，则应输出 0。

对于方程的求解，分两种情况讨论：

1. 若 $\Delta = b ^ 2 - 4ac < 0$，则表明方程无实数解，此时你应当输出 NO；

2. 否则 $\Delta \geq 0$，此时方程有两解（可能相等），记其中较大者为 $x$，则：

   1. 若 $x$ 为有理数，则按有理数的格式输出 $x$。

   2. 否则根据上文公式，$x$ 可以被唯一表示为 $x = q _ 1 + q _ 2 \sqrt r$ 的形式，其中：

      • $q _ 1, q _ 2$ 为有理数，且 $q _ 2 > 0$；
      • $r$ 为正整数且 $r > 1$，且不存在正整数 $d > 1$ 使 $d ^ 2 \mid r$（即 $r$ 不应是 $d ^ 2$ 的倍数）；

   此时：

   1. 若 $q _ 1 \neq 0$，则按有理数的格式输出 $q _ 1$，并再输出一个加号 +；
   2. 否则跳过这一步输出；

   随后：

   1. 若 $q _ 2 = 1$，则输出 sqrt({r})；
   2. 否则若 $q _ 2$ 为整数，则输出 {q2}*sqrt({r})；
   3. 否则若 $q _ 3 = \frac 1{q _ 2}$ 为整数，则输出 sqrt({r})/{q3}；
   4. 否则可以证明存在唯一整数 $c, d$ 满足 $c, d > 1, \gcd(c, d) = 1$ 且 $q _ 2 = \frac cd$，此时输出 {c}*sqrt({r})/{d}；

   上述表示中 {n} 代表整数 {n} 的值，详见样例。

   如果方程有实数解，则按要求的格式输出两个实数解中的较大者。否则若方程没有实数解，则输出 NO。

输入格式

输入的第一行包含两个正整数 $T, M$，分别表示方程数和系数的绝对值上限。

接下来 $T$ 行，每行包含三个整数 $a, b, c$。

输出格式

输出 $T$ 行，每行包含一个字符串，表示对应询问的答案，格式如题面所述。

每行输出的字符串中间不应包含任何空格。

样例 #1

样例输入 #1

9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1

样例输出 #1

1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2

提示

【样例 #2】

见附件中的 uqe/uqe2.in 与 uqe/uqe2.ans。

【数据范围】

对于所有数据有：$1 \leq T \leq 5000$，$1 \leq M \leq 10 ^ 3$，$|a|,|b|,|c| \leq M$，$a \neq 0$。

测试点编号	$M \leq$	特殊性质 A	特殊性质 B	特殊性质 C
$1$	$1$	是	是	是
$2$	$20$	否	否	否
$3$	$10 ^ 3$	是	否	是
$4$	$10 ^ 3$	是	否	否
$5$	$10 ^ 3$	否	是	是
$6$	$10 ^ 3$	否	是	否
$7, 8$	$10 ^ 3$	否	否	是
$9, 10$	$10 ^ 3$	否	否	否

其中：

• 特殊性质 A：保证 $b = 0$；
• 特殊性质 B：保证 $c = 0$；
• 特殊性质 C：如果方程有解，那么方程的两个解都是整数。

思路

按照题目思路模拟分解即可，具体注释见代码。

大坑！

!注意!，请!注意!时间!复杂度!，这是我的考场代码，复杂度为 $O(Tb^2-4Tac)$，无法通过：

 #include <bits/stdc++.h>
//蒟蒻的垃圾模拟代码
//CCF当点人罢（
//J组题这么逆天
using namespace std;
int t,m; 
inline void yls(int u,int d){
    if((u<0&&d>0)||(u>0&&d<0)) cout<<'-';
    if(d/__gcd(u,d)==1) cout<<abs(u/__gcd(u,d));
    else cout<<abs(u/__gcd(u,d))<<'/'<<abs(d/__gcd(u,d));
}
inline bool wqpf(int tr){
    return pow(floor(sqrt(tr)),2)==tr;
}
signed main(){
    ios::sync_with_stdio(0);
    freopen("uqe.in","r",stdin);
    freopen("uqe.out","w",stdout);
    cin>>t>>m;
    for(int i=1,a,b,c;i<=t;i++){
        cin>>a>>b>>c;int tr=b*b-4*a*c;
        if(tr<0) cout<<"NO"<<endl;
        else
            if(wqpf(tr)){
                if((sqrt(tr)-b)/(2*a)>(-sqrt(tr)-b)/(2*a))
                    yls(sqrt(tr)-b,2*a);
                else yls(-sqrt(tr)-b,2*a);
                cout<<endl;
            }
            else{
                if((-b)*1.0/(a*2)) yls(-b,a*2),cout<<'+';
                int ys=1;
                for(int i=1;i<=tr;i++)
                    if(!(tr%i)&&wqpf(i)) ys=max(ys,i); //这里暴力开方浪费了很多时间，考场盲目自信复杂度算错了
                tr/=ys,ys=sqrt(ys);
                if((-sqrt(tr)*ys-b)/(2*a)>(sqrt(tr)*ys-b)/(2*a)) ys=-ys;
                if(ys==a*2) cout<<"sqrt("<<tr<<")"<<endl;
                else if(!(ys%(a*2))) cout<<abs(ys/(a*2))<<"*sqrt("<<tr<<")"<<endl;
                else if(!(a*2%ys)) cout<<"sqrt("<<tr<<")/"<<abs(a*2/ys)<<endl;
                else cout<<abs(ys/__gcd(ys,a*2))<<"*sqrt("<<tr<<")/"<<abs(a*2/__gcd(ys,a*2))<<endl;
            }
    }
    return 0;
}

代码

可以看看注释，非常详细。

#include <bits/stdc++.h>
//修改过的代码，复杂度O(Tb)
using namespace std;
int t,m; 
inline void yls(int u,int d){ //输出分子为u，分母为d的有理分数 
    if((u<0&&d>0)||(u>0&&d<0)) cout<<'-'; //异号，值为负 
    //除gcd可以达到化简分数的效果 
    if(d/__gcd(u,d)==1) cout<<abs(u/__gcd(u,d)); //分母为1，输出整数形式 
    else cout<<abs(u/__gcd(u,d))<<'/'<<abs(d/__gcd(u,d)); //按照分数形式输出 
}
inline bool wqpf(int tr){
    return pow(floor(sqrt(tr)),2)==tr; //判断一个整数tr是否为完全平方数，即为判断根号是否为整 
}
signed main(){
    ios::sync_with_stdio(0);
    freopen("uqe.in","r",stdin);
    freopen("uqe.out","w",stdout); //考试的时候不要写错了啊qwq 
    cin>>t>>m;
    for(int i=1,a,b,c;i<=t;i++){
        cin>>a>>b>>c;int tr=b*b-4*a*c; //计算解的根号部分的被开方数 
        if(tr<0) cout<<"NO"<<endl; //实数范围内无解 
        else
            if(wqpf(tr)){ //根号部分是完全平方数，即有有理数解 
                if((sqrt(tr)-b)/(2*a)>(-sqrt(tr)-b)/(2*a)) //寻找最大解 
                    yls(sqrt(tr)-b,2*a); //套公式即可 
                else yls(-sqrt(tr)-b,2*a);
                cout<<endl;
            }
            else{
                if((-b)*1.0/(a*2)) yls(-b,a*2),cout<<'+';
                // 根据乘法分配律可得(-b+sqrt(tr))/2a=-b/2a-sqrt(tr)/2a
                // 即为输出解的前一项b/2a，为有理数。 
                int ys=1,rr=tr,cnt; //tr为根号下三角形的被开方数，ys为被开方数的最大完全平方因数 
                //rr作临时变量，对根式进行化简，提系数 
                for(int i=2;i*i<=rr;i++)
                    if(!(rr%i)){ //找质因数 
                        cnt=0;
                        while(!(rr%i)) rr/=i,cnt++; //化简至rr与i互质，cnt即为原数所含质因数i的个数 
                        ys*=pow(i,cnt-cnt%2); //提偶数个i出来 
                    }
                tr/=ys,ys=sqrt(ys); //化简，提出来 
                if((-sqrt(tr)*ys-b)/(2*a)>(sqrt(tr)*ys-b)/(2*a)) ys=-ys;
                //如果-b/2a-sqrt(tr)/2a是最大解时，把提出来的系数取负，直接就可以当做-b/2a+sqrt(tr)/2a 
                if(ys==a*2) cout<<"sqrt("<<tr<<")"<<endl;
                //系数为1时，直接输出根号格式 
                else if(!(ys%(a*2))) cout<<abs(ys/(a*2))<<"*sqrt("<<tr<<")"<<endl;
                //系数为整数时。注意：可以证明 sqrt(tr)/2a 一定为整，为了方便符号处理，直接取绝对值就好了 
                else if(!(a*2%ys)) cout<<"sqrt("<<tr<<")/"<<abs(a*2/ys)<<endl;
                //系数分子为1，当作除法处理 
                else cout<<abs(ys/__gcd(ys,a*2))<<"*sqrt("<<tr<<")/"<<abs(a*2/__gcd(ys,a*2))<<endl;
                //系数为分数时，按照题面格式输出为a*sqrt(c)/b的格式 	
            }
    }
    return 0;
}

T4 bus

咕咕咕。。。qwq